Engineering Assignment: Variations in Flow Rate with Differential Equations

Question

Task

Engineering Assignment Instructions: In this laboratory we will examine a system which has various attributes that are related to each other. Specifically, we will model the rate at which the level of a fluid is changing with differential equations.

There are two parts to this Laboratory, SECTION A – One question; SECTION B - Two questions. You must provide satisfactory response to all the questions in each section.

SECTION A
Experimental Apparatus
Various tanks of differing cross-sectional area are to be used.

• Round,
• Square based,
• Elliptical.

Each of these containers can be fill with water from the top; and they each have a tap on the side for draining.

Use one of the metal rulers to measure the height of the water.

Question 1
After watching the video, explain in your own words – what you perceive to be the likely challenges, when attempting to build a model of a draining tank, based on the techniques used and the data collected in the example in the video.

SECTION B
Required in your Submission for Question 2 and Question 3

For each of the following questions you must do the following:

1. Tabulate all of the information that you have been provided.

2. Derive other values, from the basic system geometry.

3. List the relevant kinematics formulas to see what might suggest itself as a way forward.

4. As the system is changing dynamically, you will need to model each system in terms of the changing variables.

5. Explain what is changing?

6. Explain in what respect is it changing?

NOTE: It is very important that you show all of your working.

You can do your working either on Word or Excel, or alternatively using pen and paper. If you use pen and paper, you must write legibly and neatly, and then must scan your assignment submission using a high resolution scanner before uploading it, as above.

Question 2
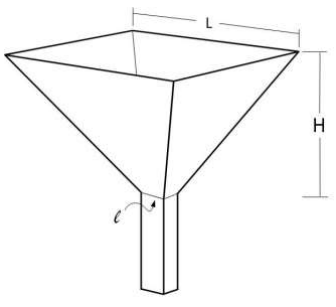
In this question, you are to model the flow of a liquid through a square based, pyramidal funnel.

The funnel is of length of side L = 550 mm and with height H to the (imaginary) apex of 450 mm.

The outlet is of length of side l = 5 mm. This question is in three parts.

Part A
Create a mathematical model of the liquid delivery through a square based pyramidal funnel. Give height in terms of time (t).

Part B
Calculate the time taken to drain the funnel from the full state. State all of the assumptions that you are using.

Part C
Create a working MATLAB program which deploys your mathematical model above.

It is important to show the steps that you have chosen to create your mathematical model of this system.

Justifications are required for why you have made the decisions that you have.

Question 3
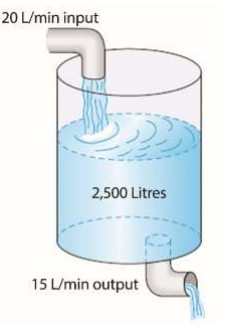
A 4,500 litre tank contains 2,500 litres of brine. There is 50 kg of salt initially present. Pure water is being put into the tank at 20 litres/min. Brine solution is draining away at a rate of 15 litres/min.

Part A
Create a mathematical model of the dissolved salt in the solution. Give amount of salt in terms of time (t).

Part B
Calculate how much salt is in the system after 15 minutes. State all of the assumptions that you are using.

Part C
Create a working MATLAB program which deploys your mathematical model above. It is important to show the steps that you have chosen to create your mathematical model of this system.

Answer

Abstract— This engineering assignment provides the variation of flow rate with various parameters, mathematical and MatLab models to find out the flow rate due to given geometry and change in the concentration due to the flow of the solution and other conditions.

Keywords— fluid, rate of flow, differential equations, modeling

Section A
This section deals with the change in height of the water in a container when it drains out from a hole of small cross-section.

Question 1:Challenges while building a model of draining the tank
In the experiment, the tank was circular-shaped based with a bottom diameter of 24 cm and a top diameter of 39 cm. The orifice was also circular with a diameter of about 1 cm with the cross-section lying vertically. It is initially filled up to 26 cm in height. Height is measured every 10 sec. Likely challenges that we might face while making a model for the draining, based on collected data and used technique, are:

1. The number of observations is less, and if the actual relation of height is of complex form, it would be difficult to model it with only these many trial points.
2. The time step is not uniform throughout the experiment. Also, there might be some lag when the timer stops and when the water flow is stopped.
3. The height was measured in the water with a regular ruler and thus if it is not perfectly perpendicular, the height measured would be inaccurate.
4. The bottom surface of the tank was not flat. It was lifted from the middle. This condition also has to be considered while making the model.

Section B
This section deals with the rate of flow and change in concentration due to flow.

Question 2: Modelling the flow of a liquid through a square-based, pyramidal funnel

Fig. 1 Shape and dimensions of the funnel used

TABLE I
Dimensions

1) To model the flow of the liquid we will need the volume of the square based truncated pyramid. Kinematic formulas involved are Bernoulli equation and flow rate equation.

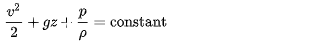
where v is fluid flow speed, g is acceleration due to gravity, z is elevation ,p is pressure and rho is the density of fluid at a given point.

(above the notation q? is used to represent dq/dt)

dV/dt is change in change in the volume of fluid and phi is the volumetric fluid rate at which the fluid goes through the orifice.

2) Assumptions taken:

1. With respect to the volume of the funnel, the volume of the neck is assumed to be negligible.
2. Fluid is incompressible and have zero viscosity
3. Since l is small in comparison to L, while applying the similarity property at some points, H could be assumed as the total height of the pyramid.
4. Surface of the liquid at the top moves very slowly
5. The square prism at the bottom could be neglected due to the reason that in a funnel, that portion is very small and therefore, the volume in it is also very small.

3) Part 1: Mathematical Model
At any time, let the height of the fluid be h(t), then the cross-sectional area could be found using the similarity property. We are taking two reference points A and B, one at the top and one at the bottom respectively.

On applying bernoulli equation we get:

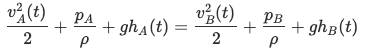
Pressure is to be the same at both points (considering assumption 05), Velocity at point A is considered to be 0 (assumption 04). From this we get vB to be equal to:

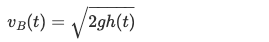
The volume of the funnel is :

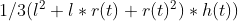
Where r(t) and h(t) are the side of the top square surface and height of the top surface and

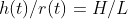
The volume comes out to be

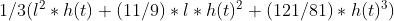
The rate of change of volume is:

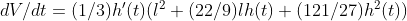
Equating it to the flow of liquid:

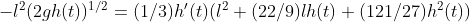
On further reduction:

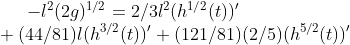
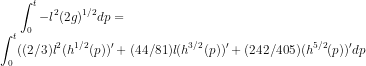
On solving this equation we get the implicit form for h(t) as:

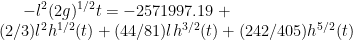
4) Part 2: Time taken for it to empty

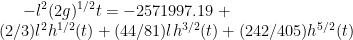
By putting the value 0 in h(t) we can find the time taken by funnel to reach an empty state. It should be noted that the unit of length is mm. So the value of g should be multiplied by 1000. (g=9860.65 mm/sec2)

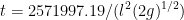
t comes out to be 734.607 sec.

5) Part 3: Matlab Model
For simulation purposes, we use numerical integration by sum method. We have chosen a unit of time dt = 0.01 sec in which we update our parameters. The truncated pyramid is extended in the bottom to complete the pyramid. This makes simulation easier and the error is insignificant due to very small volume. We initially take H,L, and Volume and then update H. Then we calculate the loss in volume of fluid and this is subtracted from the previous volume and new height is calculated for this volume. Using similarity, width is also updated after every 0.01 sec. After this we finally subtract the height by the factor with which we increased it earlier since the reference point is B where the side length is l.

Results of simulations are given below:

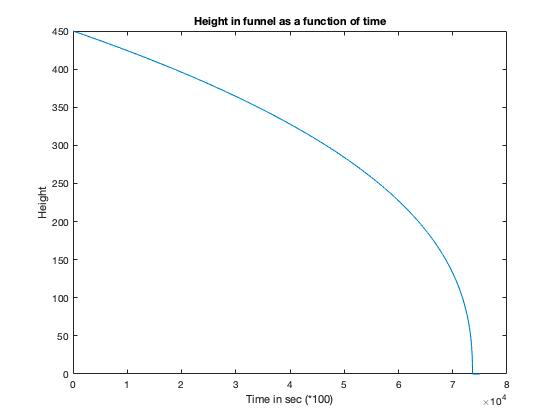
Fig. 2 Simulation for flow in funnel

T, when the funnel is empty, comes out to be 736.47 sec which is very close to the one obtained mathematically. Error is 0.2536% which is well within permissible limits.

Question 3 : Concentration change in tank due to flow of solution.

TABLE II
Dimensions And Values

Assumptions made:
The liquid is non-viscous and the concentration of the solution is uniform throughout at any given instant

Part A: Mathematical Model
To model the amount of salt left in the tank first we find the concentration in the tank and then find out the value of salt present as a function of time by multiplying it with volume.

Volume of water in the tank at a given time t is:

2500 + 5t

The concentration of the solution at any given instant by mass balancing is given by:

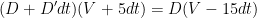
Here D is the concentration at a given time, D’ is the derivative, V is the initial volume.(New density*New volume = Old density*Volume after removal of solution)

On further solving the equation, and neglecting dDdt since it is very small and it tends to 0, we get:

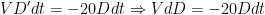
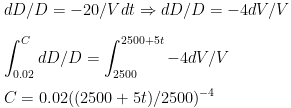
Now we have the concentration as a function of time and also the volume.

The final expression for amount of salt is given by:

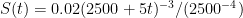
(the unit of time is min)

Part B: Amount of salt

The amount of salt in the system after 15 min can be found out by putting the value 15 in time. The unit of time in the model is minutes.

It comes out to be:

S(15) = 45.7570 kg

Part C: Matlab model
The MATLAB model is built by using the time step of 0.0001 min. For every time step, new concentration is found by using the fact that total salt is 50kg - lost due to the flow in each time step(i.e. Summation of all concentration multiplied by flow rate and time step). The total volume is 2500 + 5*total number of time steps*step size. After that, amount of salt is calculated by multiplying the concentration with volume. Concentration term was calculated because it was necessary in the iteration process.

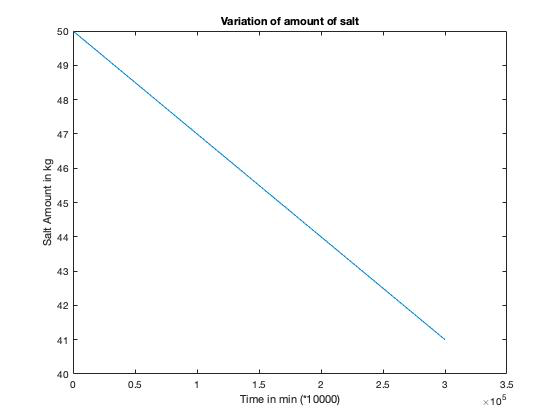
Fig. 3 Simulation for amount of salt in the tank as a function of time

Amount of salt in the system after 15 minutes by simulation was found to be 45.5 kg. Error in the result is of 0.561% which is within the permissible limits.